FastAPI – czyli jak napisać proste REST API w Pythonie? – część 1
REST API w Pythonie? Nic prostszego. Zacznij z nami już dziś swoją przygodę z FastAPI!
 Autor:
Autor:Zespół Innokrea przedstawia Wam kolejny, przedostatni odcinek serii o superkomputerach. Opowiemy o tym jak organizowana jest architektura sieciowa systemów klastrowych, o topologiach sieci, teorii grafów, a także o tym na co jeszcze zwrócić uwagę przy budowie takich systemów. Zapraszamy do lektury!
Systemy Interconnect
Wzajemne połączenia mają kluczowe znaczenie w superkomputerach, ponieważ aplikacje obliczeniowe wymagają równoległego przetwarzania ogromnych ilości danych, często przez tysiące, a nawet miliony pojedynczych elementów obliczeniowych. Jest to ważne zagadnienie ze względu na to, że przemieszczanie danych jest najbardziej kosztowną operacją w systemach równoległych pod względem wydajności.
Aby osiągnąć odpowiedni poziom równoległości, superkomputery wykorzystują wyspecjalizowane połączenia, które zapewniają komunikację o dużej przepustowości i małych opóźnieniach między poszczególnymi elementami obliczeniowymi. Istotnym elementem wpływającym na te parametry jest topologia sieci, która opisuje strukturę używaną do połączenia procesorów i przełączników.
Istnieje kilka różnych typów połączeń, które są powszechnie stosowane w superkomputerach, w tym InfiniBand, Ethernet i zastrzeżone połączenia opracowane przez dostawców, takich jak Cray i Fujitsu.
Systemy sieciowe – podstawowe elementy
Sieć interconnect składa się z następujących elementów:
Sieci Direct vs Indirect
Istotnym podziałem jeśli chodzi o sieci komputerowe w przypadku superkomputerów jest to czy sieć jest zbudowana w oparciu o połączenia z pośrednikiem czy bezpośrednie. Może to być nieco dziwne dla ludzi obcującymi na codzień ze zwyczajnymi urządzeniami sieciowymi tj. przełącznikami i routerami, ponieważ sieci domowe czy korporacyjne budujemy w oparciu o urządzenie pośredniczące. Spójrzmy na początek na definicje:
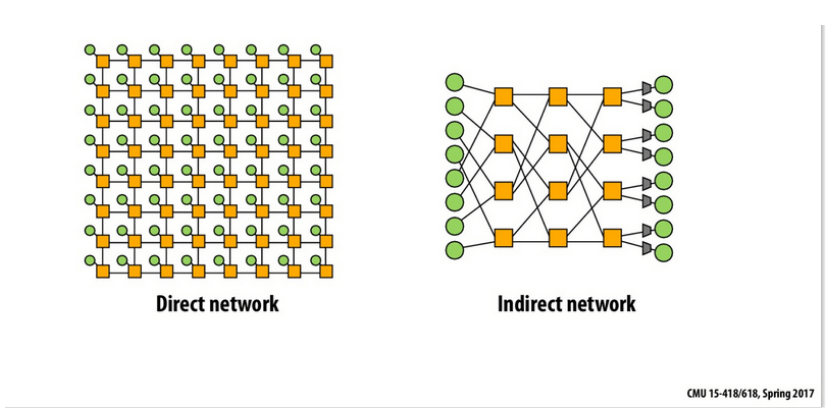
Rysunek 1: Porównanie sieci pośrednich i bezpośrednich, kolor zielony to jednostki obliczeniowe (procesory), a żółte to urządzenia pośredniczące.
W przypadku sieci bezpośredniej oba te urządzenia scalone są w jedno. Źródło: Carnegie Mellon University.
Superkomputery budowane są zarówno jako sieci bezpośrednie jak i pośrednie. Ma to związek ze stosowaną technologią oraz topologią.
Topologia sieci a teoria grafów
Dział matematyki znany jako teoria grafów jest ściśle powiązany z topologiami sieciowymi i budowaniem optymalnej sieci, szczególnie w superkomputerach, gdzie ilości węzłów są gigantyczne, a opóźnienia muszą być minimalne. Sieć może być więc reprezentowana jako graf nieskierowany, gdzie wierzchołki to węzły, a krawędzie to połączenia sieciowe. Graf nieskierowany ze względu na to, że można przesyłać wiadomości w obie strony. Chcemy, aby połączenie występowało pomiędzy dwoma dowolnymi węzłami. Charakteryzując połączenie mówimy o takich parametrach jak:
Topologie sieci bezpośrednich
Wyżej wymienione parametry z teorii grafów są wykorzystywane do określenia parametrów sieci i tego jak bardzo nadaje się ona do superkomputera czy innego systemu wysokiej wydajności.
Źródła do ilustracji dostępne są na samym dole. Nie zostały zamieszczone przy zdjęciach, żeby nie zaciemniać koncepcji.
|
Rysunek 2: Pierścień. |
Stopień: 2 Średnica: ⌊n/2⌋ Bisection bandwidth = 2
Niewykorzystywane w superkomputerach. |
|
Rysunek 3: Siatka (klika). |
Stopień: n-1 Średnica: 1 Bisection bandwidth = ⌊n/2⌋ * ⌊n/2⌋
Siatka jest optymalna z punktu widzenia wydajności, jednak jest również bardzo kosztowna ponieważ liczba krawędzi rośnie z liczbą węzłów. W praktyce rzadko używana w superkomputerach. |
|
Rysunek 4: Siatka W-wymiarowa – (mesh). |
Stopień: 4 Średnica: 2 * ⌊√n -1⌋ Bisection bandwidth = √n
Jest to topologia dobrze przystosowana do problemów w przestrzeni 2 wymiarowej jak np. Przetwarzanie obrazów. Na obrazku każdy węzeł jest jednocześnie switchem (kolor żółty) oraz endpoint’em (kolor zielony). Jest to klasyfikowane jako sieć bezpośrednia. |
|
Rysunek 5: W-wymiarowy torus. |
Stopień: 4 Średnica: 2 *⌊√n/2⌋ Bisection bandwidth = 2 * √n
Torus oferuje mniejszą średnicę i większe bisection bandwidth w porównaniu do W-wymiarowej siatki za bardzo podobny koszt. Jest to topologia często używana w superkomputerach. |
|
Rysunek 6: Fat-tree. |
Topologia Fat-Tree jest topologią drzewa. Procesory są liśćmi drzewa, a wszystkie inne węzły w drzewie to przełączniki. Główną cechą charakterystyczną Fat-Tree jest to, że każdy przełącznik w Fat-Tree ma taką samą liczbę łączy wchodzących i wychodzących. Można to interpretować jako łącza stające się grubsze, czyli mają większą przepustowość, w kierunku korzenia drzewa. Topologia używana w superkomputerach w sieciach pośrednich (ze switchami). |
Topologia Fat-Tree n-tego poziomu, może być kosztowna w praktyce, ponieważ przełączniki w kierunku korzenia drzewa stają się większe. Istnieje jednak alternatywne rozwiązanie. Polega ono tylko na zestawie przełączników o takiej samej pojemności. Należy zauważyć, że takie rozwiązanie jest w rzeczywistości topologią spine-leaf. Drzewo składa się wtedy z dwóch poziomów przełączników.
Taki Fat-Tree jest bardzo popularny w praktyce ze względu na stosunkowo niski koszt sprzętu. Jednak maksymalny rozmiar takiej sieci jest ograniczony liczbą portów przełączników użytych w sieci.
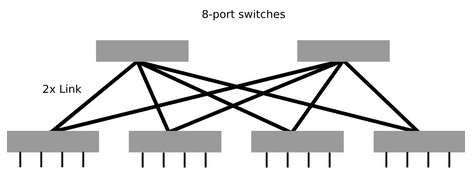
Rysunek 7: 2-poziomowy Fat Tree.
Dla 2 poziomowego fat-tree można wyliczyć zależności z następujących wzorów:
Gdzie k to liczba portów w przełączniku. Dodatkowo dla 2-warstwowego Fat-Tree parametry Diameter oraz bisection bandwidth wynoszą:
Są to dobre parametry – mały diameter oraz wysokie bisection bandwidth, dlatego jest to topologia bardzo często spotykana w superkomputerach, szczególnie tych powiązanych z technologią Infiniband.
Topologie są przedmiotem badań naukowych, co więcej badaniu podlega także ich kontekst w programowaniu równoległym. Tutaj przykład pewnego artykułu prezentowanego na konferencji o superkomputerach, gdzie autorzy proponują optymalizacje związane z MPI w kontekście topologii dragonfly.

Rysunek 8: Topologia dragonfly vs MPI.
To przedostatni wpis naszej serii o superkomputerach. Jak widać temat jest dość skomplikowany i stanowi cały dział nauki przy którym pracują zarówno specjaliści komputerowi, od programistów po sieciowców jak i matematycy starający się zaproponować teoretyczne usprawnienia. W następnym artykule opowiemy Wam o Infiniband oraz RDMA, czyli o konkretnych technologiach wykorzystywanych do zwiększenia prędkości i zmniejszenia opóźnień w ramach systemów wysokiej wydajności.
Źródła (także dla wykorzystanych rysunków):

FastAPI – czyli jak napisać proste REST API w Pythonie? – część 1
REST API w Pythonie? Nic prostszego. Zacznij z nami już dziś swoją przygodę z FastAPI!
Programowanie
2024-07-18

Dockeryzacja frontendu – zrób to dobrze React.js + Vite
Zrób to dobrze! Gotowy poradnik do dockeryzacji React.js z Vite.
Programowanie
2024-07-04
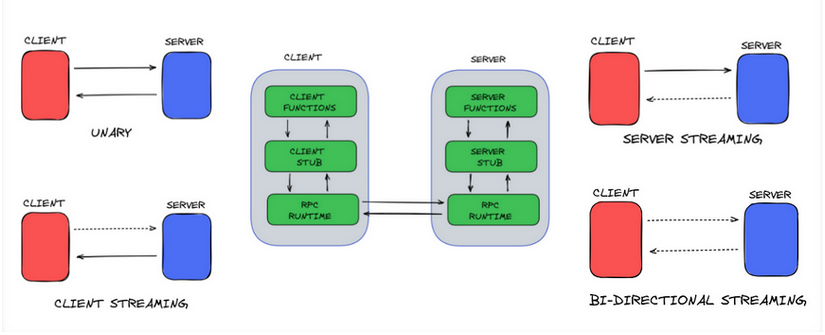
Czym jest RPC, serializacja, komunikacja międzyprocesowa oraz jak wiąże się to z systemami rozproszonymi?
AdministracjaProgramowanie
2024-06-20