Sieci neuronowe: pod lupą

Tydzień temu w naszym cyklu ML udało nam się przybliżyć przebieg tego jak trenować sieci neuronowe – jakie ma fazy, jak należy dzielić zbiór danych i dlaczego powinno się bieżąco monitorować przebieg takiego treningu. Dziś chcemy odkryć przed Wami nieco więcej szczegółów – przeanalizujemy, co właściwie zachodzi w sieci neuronowej podczas jednej epoki treningu. Zapraszamy!

Krok w przód, krok w tył

Na wstępie zaznaczyć trzeba jedno – choć generalna koncepcja treningu sieci neuronowych jest raczej jedna, to jej wariantów jest naprawdę wiele. Dzisiaj przeanalizujemy jeden z najprostszych – czyli poprawianie wag i biasów modelu każdorazowo po zaprezentowaniu jednej próbki z treningowej części zbioru (w literaturze to podejście określane jest jako stochastic gradient descent – SGD).

To powiedziawszy – czas przejść do rzeczy! Przeanalizujmy, jakie kroki zachodzą w modelu sieci neuronowej podczas jednej epoki treningu:

1. Konkretna próbka (wektor liczb) z części treningowej wczytywana jest na warstwę wejściową modelu. 
2. Dane wejściowe “przechodzą” przez kolejne warstwy sieci, gdzie poddawane są rozmaitym operacjom, na zmianę liniowym oraz nieliniowym.
3. Na warstwie wyjściowej produkowane są prawdopodobieństwa przynależności przetwarzanej próbki do każdej z rozważanych klas (każdy neuron warstwy wyjściowej reprezentuje jedną klasę).
4. Na podstawie znanej etykiety (znanej właściwej klasy) próbki określane jest za pomocą funkcji straty to, jak bardzo model się “pomylił”.
5. Następnie obliczany jest gradient – pochodna funkcji straty po wszystkich parametrach (wagach) sieci – w dużym uproszczeniu można uznać, że ta wielowymiarowa pochodna pozwala nam określić, w jakim stopniu dany parametr miał wpływ na wartość funkcji straty (czyli błędu popełnianego przez model w obecnym stanie) i jak należy go poprawić.
6. Na podstawie określonego gradientu modyfikujemy parametry sieci.
   
   

Kroki 1-4 określa się często jako forward pass / propagation (przejście w przód), natomiast kroki 5-6 jako backward pass / propagation (propagacja wsteczna).

Zauważmy, że kroki 1-3 to mechanizm taki sam, jak w przypadku predykcji na już gotowym modelu (przedstawiony 2 artykuły temu – jeżeli jeszcze nie mieliście okazji, to zachęcamy do zapoznania się!).

Sieci neuronowe i warstwy – jak konstruować?

Warto tu zwrócić uwagę na jeszcze jedną rzecz, dotyczącą samej architektury sieci neuronowej: podczas, gdy tak zwane ukryte warstwy sieci mogą zawierać dowolną (w granicach rozsądku) liczbę neuronów – choć zazwyczaj przyjmuje się potęgi liczby 2 za dobry wyznacznik ich liczności – to jeżeli chodzi o warstwę wejściową oraz wejściową, obowiązują sztywne zasady:

• warstwa wejściowa zawierać musi tyle neuronów, ile elementów ma wektor wejściowy (na tej warstwie, wyjątkowo, nie dzieją się żadne z operacji opisanych w poprzednim artykule – jako, że tutaj do każdego neuronu wchodzi tylko jedna wartość – do n-tego neuronu warstwy wejścia przekazuje się jedynie n-ty element wektora)
• na warstwie wyjściowej znajdować się musi tyle neuronów, ile klas rozpoznajemy w zadaniu – jako, że każdy neuron reprezentuje jedną z tych klas (a w zasadzie prawdopodobieństwo należenia danej próbki do konkretnej z klas).

Wróćmy zatem na chwilę do grafiki z jednego z poprzednich artykułów obecnego cyklu:

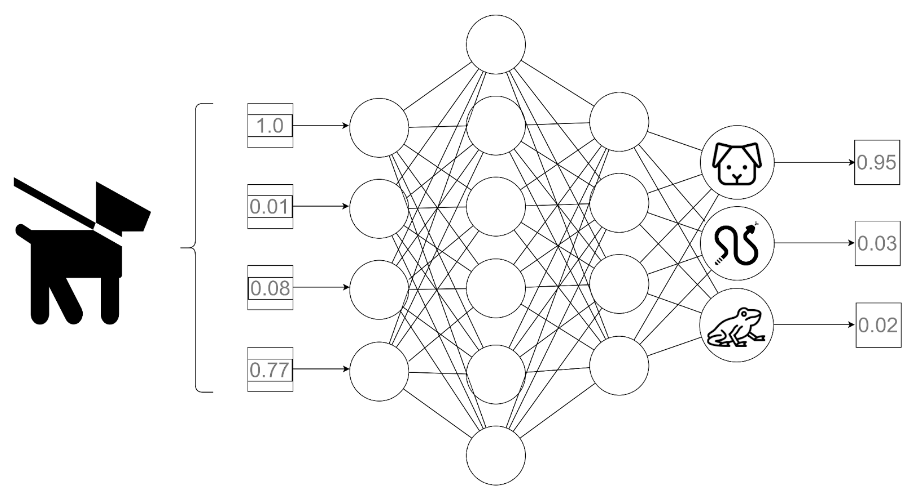
Rys. 1: Przykład działania forward pass prostej sieci

Przeanalizujmy pod lupą, co dokładnie dzieje się podczas forward pass na ukrytych warstwach:

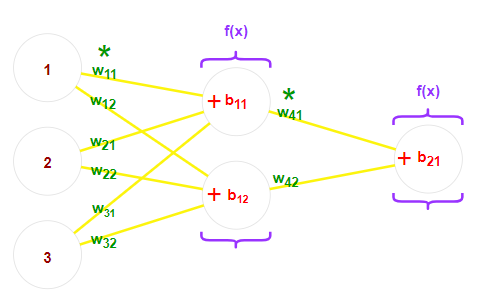
Rys. 2: „Szkolne” sieci neuronowe i ich parametry – uwagi oznaczono na zielono, biasy – czerwono, a funkcję aktywacji – fioletowo

Wartości zwracane przez neurony z warstwy wejściowej “podróżują” za pomocą połączeń do każdego z neuronów kolejnej warstwy. Każde połączenie ma wagę W, przez którą przetwarzana wartość jest mnożona. 

Na wejściu do neuronu kolejnej warstwy, wszystkie wchodzące wartości pomnożone przez właściwe wagi są sumowane. Do tej sumy dodaje się także wartość biasu B konkretnego neurona.

Powstała w tej sposób suma przekazywana jest do funkcji aktywacji A. Zadaniem takiej funkcji jest przełamanie liniowości wykonywanych operacji. Co to oznacza?

Zauważmy, że dotychczas wykonywane operacje (mnożenie oraz dodawanie) modyfikowały wartości wejścia w sposób liniowy. Gdybyśmy kontynuowali jedynie takie traktowanie danych, to każda kolejna warstwa byłaby przekształceniem liniowym wyniku warstwy poprzedniej – który też przecież powstał w wyniku operacji liniowych! Matematyka nie pozostawia złudzeń w tym zakresie – złożenie funkcji liniowych, niezależnie od ich liczby – jest również tylko funkcją liniową! Oznacza to, że bez wprowadzania funkcji aktywacji, które burzą liniowość naszej struktury – cała, wielka sieć neuronowa mogłaby tak naprawdę zostać zastąpiona… Jedną funkcją postaci f(x) = ax + b. A choć funkcje liniowe są – wbrew pozorom – potężnym narzędziem statystycznym, to jednak konstruowanie jej poprzez budowanie obszernych, sztucznych sieci neuronowych… Cóż, brzmi jak zbyt duży kaliber na to zadanie.

Sieci neuronowe – to jak z tą aktywacją?

Po tej, dość szerokiej, dygresji – przybliżmy sobie, jak zazwyczaj wygląda taka funkcja aktywacji.

Funkcje aktywacji możemy podzielić na te dotyczące:

• warstw ukrytych
• warstwy wyjściowej.

W pierwszym przypadku, jej celem jest wspomniane zaburzenie liniowości, w drugim natomiast – przekształcenie wyników w dziedzinę prawdopodobieństwa (co zazwyczaj oznacza przeskalowanie wartości do przedziału [0 ,1]).

Na warstwach ukrytych najpowszechniej stosowana jest funkcja ReLU:

f(x) = max(0, x).

Funkcja ta zachowuje zależność liniową dla wartości większych lub równych zeru, natomiast wszelkie wartości ujemne zaokrągla właśnie do niego.

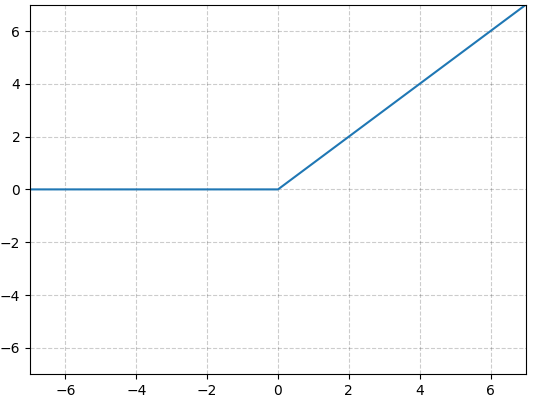
Rys. 3: Wykres funkcji ReLU

Na ostatniej warstwie, funkcję wybieramy w zależności od zadania:

• dla klasyfikacji binarnej, częstym wyborem jest funkcja sigmoid, zwracająca wyniki z przedział (0, 1) – przeważnie wyniki mniejsze od 0.5 interpretujemy jako przynależność do jednej z klas, a pozostałe – do drugiej.

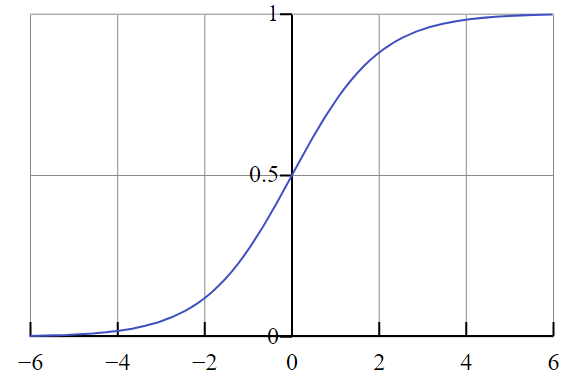
Rys. 4: Wykres funkcji sigmoid (źródło: Wikipedia.org)

• w przypadku, kiedy mierzymy się z wieloma klasami bardzo przydatna i chętnie stosowana jest funkcja softmax, która przekształca wartości neuronów na ostatniej warstwie tak, by sumowały się one do 1. Jest to funkcja dość unikatowa, ponieważ nie działa dla izolowanego neuronu, a dla wszystkich z warstwy wyjściowej naraz.
  
  

Spojrzeć prawdzie w oczy – funkcja straty i propagacja wsteczna

Udało nam się uzyskać wyniki. Teraz pozostaje sprawdzić tylko – jak dalekie od prawdy one są?

W tym celu z pomocą przychodzi nam tzw. funkcja straty – pozwala ona określić, jak duży błąd popełniła nasza sieć, porównując uzyskane wyniki z prawdziwymi (tzw. ground truth). Często stosowane są tu funkcja zwane cross entropy lub categorical cross entropy. Od tego miejsca jednak nie będziemy wchodzić już w matematyczne szczegóły – jako, że wymagałoby to konkretnego przygotowania matematycznego, a artykuł ten jest raczej dość ogólnym wstępem

Ostatnim krokiem fazy dostosowywania parametrów w epoce jest właśnie propagacja wsteczna – obliczenie dla każdego parametru sieci pochodnej po wyliczonej funkcji straty, wyznaczającej, w którym kierunku i jak bardzo należałoby daną wagę lub bias poprawić, aby wynik był bliższy prawdzie. Po obliczeniu takiej wielowymiarowej pochodnej (gradientu) dla wszystkich trenowalnych parametrów sieci, ich wartości ulegają poprawie (jak gwałtownej? Zależy to od ustalonej wartości współczynnika uczenia, ang. learning rate).

To już wszystko na dziś! Do zobaczenia za tydzień, gdzie opowiemy o metodach przyspieszania i poprawiania treningu, a także dowiemy się, że żadna sieć nie jest nieomylna – nie może Was zabraknąć!